Теория управления. Принципы системного анализа

Например, все три фигуры на рис. 4 изображают один и тот же граф.

Рис. 4. Графы

Рассмотрим процесс соединения точек А, Б, В, Г, Д ребрами.

1. Ситуация, соответствующая моменту, когда рукопожатия еще не совершались, представляет собой точечную схему, изображенную на рис. 2. Такая схема, состоящая из «изолированных» вершин, называется нулевым графом.

2. Ситуация, когда совершены еще не все рукопожатия, может схематически быть изображена, например, с помощью рис. 3: пожали руки А и Б, А и Г, Д и Г, В и Д. Графы, в которых не построены все возможные ребра, называются неполными графами.

3. На рис. 5 изображен граф, соответствующий всем совершенным рукопожатиям. Этот граф является полным графом.

Рис. 5. Полный граф с пятью вершинами

Если подсчитать число ребер графа, изображенного на рисунке, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10.

Заметим, что если полный граф имеет n вершин, то количество ребер будет равно n(n-1)/2.

На рисунке 4 ребра превращающие граф в полный граф изображены другим цветом, совокупность вершин графа с этими ребрами называется дополнением графа.

Степень вершины – количество ребер графа, исходящих из этой вершины.

На рис. 3 изображен граф с пятью вершинами. Степень вершины А обозначим Ст.А. На рис. 4: Ст.А = 2, Ст.Б = 1, Ст.В = 1, Ст.Г= 2, Ст.Д= 2.

Вершина называется нечетной - если степень этой вершины нечетная, четной - если степень этой вершины четная.

Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.

Введем понятие ориентированного графа. В таком графе дуги имеют стрелки, направленные от одной вершины к другой (рис. 6).

Рис.6. Примеры ориентированных графов

Ориентированный граф был бы полезен, например, для иллюстрации организации перевозок в транспортной задаче. В экономике дугам ориентированного или обычного графа часто приписывают числа, например, стоимость проезда или перевозки груза из пункта А (начальная вершина дуги) в пункт Б (конечная вершина дуги)

Путем в графе от одной вершины к другой называется такая последовательность ребер, по которой можно проложить маршрут между этими вершинами, при этом никакое ребро маршрута не должно встречаться более одного раза. Вершина, от которой проложен маршрут, называется началом пути, вершина в конце маршрута — конец пути. Простой путь – путь, в котором ни одна дуга не встречается дважды. Элементарный путь – путь, в котором ни одна вершина не встречается дважды. Контур – путь, у которого конечная вершина совпадает с начальной вершиной. Длиной пути (контура) называется число дуг пути (или сумма длин его дуг, если последние заданы).

Циклом называется путь, в котором совпадают начало с концом. Если все вершины цикла разные, то такой цикл называется элементарным (или простым) циклом. Если же цикл включает в себя все ребра графа по одному разу, то такой цикл называется Эйлеровой линией. На рис. 7 приведены примеры Эйлеровых линий.

Рис. 7. Примеры Эйлеровой линии

Элементарный путь (контур), проходящий через все вершины графа, называется гамильтоновым путем (контуром).

Две вершины графа называются связными, если в графе существует путь с концами в этих вершинах. Если такого пути не существует, вершины называются не связными.

Так, на рис. 8 любая пара вершин, взятая из набора А,Б,В,Г,Д, будет связной, т.к. от любой из них к любой можно "пройти" по ребрам графа. Пары вершин, одна из которых взята из набора А,Б,В,Г,Д, а другая из набора Е,Ж,З, не будут связными, т.к. от одной к другой "пройти" по ребрам не удается.

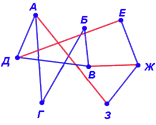
Рис. 8. Примеры связных и несвязных графов

Граф называется связным, если любая пара его вершин — связная.

Граф называется несвязным, если в нем есть хотя бы одна несвязная пара вершин.

На рис.8, очевидно, изображен несвязный граф. Если, например, на рис. 8 между вершинами Д и Е провести ребро, то граф станет связным. Такое ребро в теории графов, после удаления которого, граф из связного превращается в несвязный, называется мостом.

Примерами мостов на рис. 8 могли бы служить ребра ДЕ, AЗ, ВЖ и др., каждое из которых соединяло бы вершины «изолированных» частей графа.

Деревом называется любой связный граф, не имеющий циклов. Договорились считать «деревом» и всякий граф, состоящий из одной (изолированной) вершины.

Рис. 9. Дерево

На рисунке приведен пример графа «дерева». Вершина дерева, имеющая степень единицу, называется висячей вершиной (на рис. 9 они отмечены кружком).

Рассмотрим несколько типичных задач принятия решений, связанных с оптимизацией на графах:

1. Задача о кратчайшем пути.

2. Задача о максимальном потоке.

3. Задача коммивояжера.

Задача о кратчайшем пути

Как кратчайшим путем попасть из одной вершины графа в другую (следовательно, с наименьшим расходом топлива и времени, наиболее дешево попасть из пункта А в пункт Б)? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число – время движения по этой дуге от начальной вершины до конечной (рис. 10).

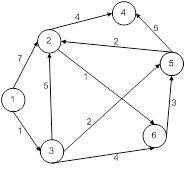
Рис. 10. Исходные данные

Ситуацию можно описать не только ориентированным графом с весами, приписанными дугам, но и таблицей (табл. 1).

Табл. 1. Исходные данные к задаче о кратчайшем пути