Теория управления. Принципы системного анализа

т. е. получили нормированное значение собственного вектора.

Для получения max выполним следующие шаги:

1. Определим сумму элементов для каждого столбца матрицы R:

2. Определим скалярное произведение векторов:

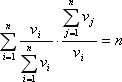
что соответствует максимальному собственному числу для идеально согласованной матрицы.

Итерационный метод основан на следующей теореме:

Для положительной квадратной матрицы R собственный вектор V, соответствующий максимальному собственному значению max, с точностью до постоянного сомножителя C определяется по формуле:

где e = (1, 1, ., 1)T - единичный вектор

k = 1, 2, 3,… показатель степени

C – константа

Т – знак транспонирования

Вычисление собственного вектора V производится до достижения заданной точности:

eT|V(l) - V(l-1)| 

где l – номер итерации, такой, что l = 1 соответствует k = 1; l = 2, k = 2 и т. д.

 - допустимая погрешность

С достаточной для практики точностью принимается равной 0,01 независимо от порядка матрицы.

Максимальное собственное значение вычисляется по формуле:

max = eTRV

3. Принцип синтеза

Реализация принципа синтеза составляет содержание третьего этапа. Искомые веса объектов определяются последовательно, начиная со второго уровня иерархии в соответствии с решающим правилом

(9)

Рис. 17. Фрагмент иерархии

Веса объектов, принадлежащих уровню альтернатив, можно считать как результат измерения их в шкале отношений в диапазоне [0,1].

Согласованность всей иерархии С определяется по следующему выражению:

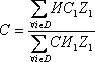(10)

где D = I / Vm; ИСi, СИi, - соответственно индекс согласованности и случайный индекс таблицы парных сравнений, рассмотренной относительно i-го объекта. Если i  V1 и i > 1, то для i  V1 ИСi = ИС1 и СИi = СИ1; ИС1 и СИ1 - соответствующие параметры таблицы парных сравнений, которая была сформирована для определения весов объектов первого уровня.

Приемлемым является значение С меньше или равное 10%. В противном случае качество суждений следует улучшить. Возможно, следует пересмотреть формулировку вопросов при проведении парных сравнений. Если это не поможет улучшить согласованность, то, вероятно, задачу следует более точно структурировать.

14.10 Общая оценка МАИ как метода принятия решений

Принятие решений складывается в многодисциплинарную область исследований, в которой работают психологи, математики, программисты, экономисты, инженеры. Отметим, что эта многодисциплинарность является как бы переходным этапом к появлению новой дисциплины, в рамках которой специалисты будут обладать необходимыми научными знаниями из приведенных выше дисциплин, а также новыми знаниями по проблемам, ранее не изучавшимся.

Рассмотрим, насколько удовлетворяет МАИ ряду требований к научному обоснованию методов принятия решений:

1. В МАИ способы получения информации от ЛПР/эксперта соответствуют данным когнитивной психологии о возможностях человека перерабатывать информацию. Действительно, гомогенность и принцип иерархической декомпозиции приводят в соответствие проблему получения оценок с психометрическими возможностями человека.

2. В МАИ имеется возможность проверки информации, полученной от ЛПР/эксперта на непротиворечивость, посредством индекса и отношения согласованности как для отдельных матриц, так и для всей иерархии.

3. Любые соотношения между вариантами решений в МАИ объяснимы на основе информации, полученной от ЛПР/экспертов. Так, анализ весов объектов по нисходящим уровням иерархии позволяет понять, как получено то или иное значение веса.

4. Математическая правомочность решающего правила в МАИ прозрачна и базируется на методе собственных значений и принципе иерархической композиции, имеющих четкое математическое обоснование.

Таким образом, МАИ удовлетворяет четырем основным критериям обеспечивающим всестороннюю научную обоснованность метода принятия решений.

Решающим преимуществом МАИ над большинством существующих методов оценивания альтернатив является вклад в анализ структуры проблемы и отчетливое выражение суждений.

Сложность, как было уже отмечено, характеризуется большим числом взаимодействий между многими субъективными и объективными факторами различного типа и степени важности, а также группами людей с различными целями и противоречивыми интересами. Эти факторы определяют вероятность или невозможность выбора одной из альтернатив, которая приемлема для всех с определенной степенью компромисса.

Чтобы разобраться с этой сложностью, нужна систематическая процедура для представления групп, их целей, критериев и поведения, обусловленных этими целями, альтернативных исходов и ресурсов, распределяемых по этим альтернативам. В МАИ эта процедура сводится к построению иерархии проблемы.

Общая цель (фокус) проблемы (например, выбор наилучшего автомобиля, построение наилучшей системы, распределение ресурса в соответствии с важностью) является обычно высшим уровнем иерархии. За фокусом следует уровень наиболее важных критериев (таких, как стоимость, стиль, комфортабельность и размеры автомобиля, или же в планировании - прибыльность инвестиции, конкуренция и т.д.). Каждый из критериев может разделяться на субкритерии. За субкритериями следует уровень альтернатив, число которых может быть очень большим.

Как будет показано, в некоторые иерархии может быть включен уровень действующих сил (акторов), который расположен ниже уровня общих критериев. Уровень определяет, какой из акторов наибольшим образом воздействует на исход. За этим уровнем для каждого актора следует уровень целей акторов, за которым следует уровень политик акторов, и далее уровень альтернативных исходов.

В общем, декомпозиция проблемы в иерархию зависит от хода мыслей ЛПР (его концепции решения проблемы), интуиции и опыта.

С целью иллюстрации этапов МАИ рассмотрим задачу о выборе работы.

Пример 1

Со студентом, только что получившим диплом, беседовали о трех возможных местах работы (А, Б и В). Он решил использовать МАИ для осуществления выбора. В результате первого этапа применения МАИ была получена следующая иерархия.

Рис. 17. Иерархия проблемы выбора работы

Уровень цели:

1. Удовлетворение работой.