Теория управления. Принципы системного анализа

В конкретной практической ситуации для выбора подходящей дробной реплики полного факторного плана необходимо использовать все априорные сведения теоретического и интуитивного характера об объекте планирования с целью выделения тех факторов и произведений факторов, влияние которых на результаты измерений существенно. При этом смешивание нужно производить так, чтобы общее среднее b0 и главные эффекты b1, ., bm были смешаны с эффектами взаимодействий самого высокого порядка (так как обычно они отсутствуют) или с эффектами таких взаимодействий, о которых известно, что они оказывают несущественное влияние на результаты измерений. Отсюда следует, в частности, что недопустимо произвольное разбиение полного факторного плана 23 на две части для выделения полуреплики 23-1.

Качество дробного факторного плана иногда характеризуют с помощью разрешающей способности плана, которая равна наименьшему числу символов в правых частях определяющих соотношений. В частности, для плана разрешающей способности III ни один главный эффект не смешан ни с каким другим главным эффектом, но главные эффекты смешаны с эффектами двухфакторных взаимодействий. Для плана разрешающей способности IV главные эффекты не смешаны друг с другом и с эффектами двухфакторных взаимодействий, но последние друг с другом смешаны. Для плана разрешающей способности V главные эффекты и эффекты двухфакторных взаимодействий не смешаны, но последние смешаны с эффектами трехфакторных взаимодействий. Все три рассмотренные выше дробные реплики имеют разрешающую способность III.

Метод наименьших квадратов

Рассмотрим особенности регрессионного анализа результатов моделирования на примере построения линейной регрессионной модели.

На рис. 3.9 показаны точки (xi, yi), полученные в эксперименте. Делаем предположение, что функция отклика может быть представлена в виде прямой линии

Требуется получить такие значения коэффициентов b0 и b1, при которых сумма квадратов ошибок будет минимальной. На рисунке ошибки ei для каждой экспериментальной точки равны расстояниям по вертикали от этой точки до линии регрессии (рис. 3).

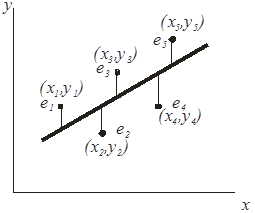
Рис. 3.К построению регрессионной модели

Обозначим (yt)i =b0+ b0xi (здесь (уt)i - величина, предсказываемая регрессионной моделью), тогда выражение для ошибок будет иметь вид а функция ошибки

Для получения коэффициентов b0 и b1 при которых функция F0 будет минимальной, приравняем нулю частные производные dF0 /db0 и dF0 /db1. Будем иметь:

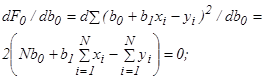
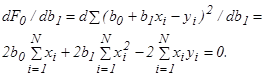(20)

Таким образом, получена система двух линейных алгебраических уравнений:

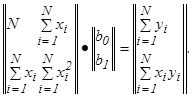(21)

Решая систему этих уравнений, получим

(22)

где N – число реализаций при моделировании.

Мы рассмотрели частный случай для уравнения (22). В более общем случае, когда эмпирическую функцию принимают в виде полинома

(23)

система уравнений типа (22), (23) будет иметь вид

(24)

Для оценки точности совпадения теоретических и экспериментальных данных следует определить среднюю квадратичную ошибку на единицу веса

(25)

или среднее абсолютное отклонение

(26)

где r – число вычисляемых (табличных) значений;

s – число параметров.

Последовательность вычислений при построении уравнения регрессии на основе метода наименьших квадратов рассмотрим на конкретном примере.

Пусть например необходимо подобрать уравнение регрессии по экспериментальным данным, приведенным ниже.

Вначале попытаемся в качестве типа эмпирической формулы принять линейную зависимость, удерживая в формуле два первых члена:

Составим нормальные уравнения, для чего предварительно заполним таблицу В таблице предусмотрим дополнительные столбцы 4, 5 и 8, которые нам могут потребоваться в дальнейшем (таблица 7).

Таблица 7