Теория управления. Принципы системного анализа

Примером механической поступательной системы (рис. 8) служит автомобиль массой , который перевозит груз массой и прицеп массой . В прицепе находится подпружиненный груз массой .

Рис. 8.Поступательная механическая система и её эквивалентная схема:

На рисунке F – тяга автомобиля; и – приведенные коэффициенты трения между грузами и кузовами автомобиля и прицепа; и – упругости сцепления и пружины крепления груза к прицепу

В качестве примера системы, состоящей из электрической, механической и пневматической подсистем, рассмотрим вибронасос (рис. 9). Под воздействием переменного магнитного поля, возникающего в зазоре электромагнита, приходит в движение груз массой т. Этот груз, шарнирно связанный через рычаг с насосом, действует на сильфон S, который, пульсируя, прокачивает воздух через клапаны k.

Рис. 9.Схема вибронасоса

В устройстве можно выделить конструктивно самостоятельные простые подсистемы, доказанные на эквивалентной схеме замещения (рис. 10): обмотку электромагнита 1, электромагнит 2, рычажный механизм 3, сильфон и воздушную магистраль с клапаном Связи этих подсистем осуществляются гираторами для пар 1-2 и 3-4 и трансформатором – для пары 2-3.

Рис.10.Эквивалентная схема замещения вибронасоса

Метод получения топологических уравнений

Эквивалентная схема технической системы может быть представлена в виде графа, ребра которого изображают двухполюсники, замещающие элементы (компоненты) системы. Пусть задан граф (рис. 11) некоторой технической системы. Топологические уравнения равновесия (типа уравнений первого закона Кирхгофа) могут быть записаны для каждого сечения, которое может включать один или несколько узлов. Для узлов, отмеченных на рис. 11, можем записать (принимая знак минус при направлении ребер к рассматриваемому узлу) следующие уравнения:

сечение 1 ;

сечение 1-5 ;

сечение 2 (11)

сечение 4 .

Топологические уравнения неразрывности (аналоги второго закона Кирхгофа) будут иметь вид:

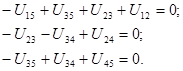(12)

Процедура получения уравнений (11), (12) может быть формализована. Для этой цели вводят матрицу контуров и сечений – М-матрицу. Такую матрицу строят с помощью ориентированного графа эквивалентной схемы и выбранного для этого графа дерева. Количество столбцов матрицы соответствует числу ветвей дерева, а количество строк – числу хорд.

Рис.11.Граф эквивалентной схемы

При формировании М-матрицы хорды поочередно включают в дерево с образованием замкнутого контура. При обходе этого контура в направлении включенной хорды формируют строку матрицы. В столбцах матрицы, соответствующих ветвям дерева, ставят +1 при совпадении направления ветви с направлением обхода и -1, если направления противоположны.

Рассмотрим построение М-матрицы (табл. 1) для графа, показанного на рис. 11. Принимая пятый узел за базовый, построим дерево графа (рис. 12). При подключении хорды 1-2 образуется контур 1-2, 2-3, 3-5, 1-5,поэтому в первой строке матрицы будем иметь - 1 (для ветви 1-5), + 1 (для ветвей 2-3, 3-5) и 0 (для ветви 3-4). Аналогично заполняют остальные строки.

Таблица 10.2

Топологические уравнения с использованием М-матрицы имеют вид:

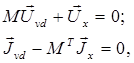(13)

где – векторы переменных типа разности потенциалов на ветвях дерева и хордах;

– векторы переменных типа потока для ветвей дерева и хорд.

Записывая первое уравнение (13) в развернутом виде

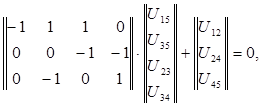
вы можете убедиться, что оно совпадает с системой уравнений (12). Аналогично, второе уравнение (13) совпадает с (11). Таким образом, использование М-матрицы позволяет формализовать процедуру получения математической модели. При этом сечения дерева специально выбирать не надо. Выше такие сечения приведены для наглядности.

Рис.12. К построению М-матрицы

Возможна иная формализация процедуры построения математической модели с использованием матрицы инциденций. Будем рассматривать исходный граф (см. рис, 11) как хорды некоторого фиктивного дерева (рис. 13), ветви которого на рисунке изображены пунктирными линиями.

Составим М-матрицу, поочередно включая в фиктивное дерево хорды исходного графа. Так, контур 1-5 состоит из хорды 1-5 и ветви 1-5, направление которой противоположно хорде, поэтому в М-матрице этой ветви будет отвечать значение – 1. В контуре 2-3-5 направление ветви 3-5 совпадает с направлением хорды, а для ветви 2-5 – не совпадает, поэтому будем соответственно иметь +1 и -1. Включая последовательно все хорды, получим М-матрицу (рис. 13), приведенную в табл. 2, или, выделяя содержательную часть М-матрицы.

Рис.13.Граф с фиктивным деревом

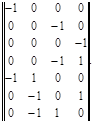(14)