Спрашивается: как кратчайшим путем попасть из вершины 1 в вершину 4?
Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается.
Для исходных данных, представленных на рис. 10 и в табл. 1, в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому С(3) = 1. Кроме того, очевидно, что С(1) = 0.
В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение
С(4) = min {С(2) + 4; С(5) + 5}.
Таким образом, проведена реструктуризация задачи - нахождение С(4) сведено к нахождению С(2) и С(5).
В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение
С(5) = min {С(3) + 2 ; С(6) + 3}.
Мы знаем, что С(3) = 1. Поэтому
С(5) = min {3 ; С(6) + 3}.
Поскольку очевидно, что С(6) - положительное число, то из последнего соотношения вытекает, что С(5) = 3.
В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение
С(2) = min {С(1) + 7; С(3) + 5; С(5) + 2}.
Нам известно, что С(1) = 0, С(3) = 1, С(5) = 3. Поэтому
С(2) = min {0 + 7; 1 + 5; 3 + 2} = 5.
Теперь мы можем найти С(4):
С(4) = min {С(2) + 4; С(5) + 5} = min {5 + 4; 3 + 5} = 8.
Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков:
1 → 3 → 5 → 4 .
Задача о кратчайшем пути для конкретных исходных данных (рис.10 и табл. 1) полностью решена.
Задача о максимальном потоке
По каким маршрутам послать максимально возможное количество грузов из начального пункта в конечный, если пропускная способность путей между пунктами ограничена?
Для решения этой задачи каждой дуге ориентированного графа, соответствующего транспортной системе, должно быть сопоставлено число – пропускная способность этой дуги (рис. 11).
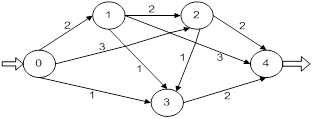
Рис. 11. Исходные данные
Исходные данные о транспортной системе, например, внутризаводской, приведенные на рис.11, можно также задать таблицей (табл. 2).
Табл. 2. Исходные данные к задаче о максимальном потоке
|
Пункт отправления |
Пункт назначения |
Пропускная способность |
|
0 |
1 |
2 |
|
0 |
2 |
3 |
|
0 |
3 |
1 |
|
1 |
2 |
4 |
|
1 |
3 |
1 |
|
1 |
4 |
3 |
|
2 |
3 |
1 |
|
2 |
4 |
2 |
|
3 |
4 |
2 |
Решение задачи о максимальном потоке может быть получено из следующих соображений.
Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3.
Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу - в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4). В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 3. Их направляем в пункт 4.
Итак, максимальная пропускная способность рассматриваемой транспортной системы - 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 - по ней направлены 2 единицы груза при пропускной способности в 3 единицы.
Решение можно представить в виде таблицы (табл. 2) или графа (рис. 12).
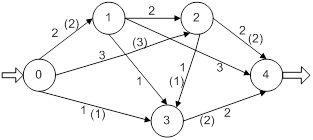
Рис. 12. Решение задачи (числа в скобках)
Табл. 3. Решение задачи о максимальном потоке
|
Пункт отправления |
Пункт назначения |
Пропускная способность |
План перевозок |
|
0 |
1 |
2 |
2 |
|
0 |
2 |
3 |
3 |
|
0 |
3 |
1 |
1 |
|
1 |
2 |
4 |
0 |
|
1 |
3 |
1 |
0 |
|
1 |
4 |
3 |
2 |
|
2 |
3 |
1 |
1 |
|
2 |
4 |
2 |
2 |
|
3 |
4 |
2 |
2 |
Дадим формулировку задачи о максимальном потоке в терминах линейного программирования. Пусть ХKM - объем перевозок из пункта К в пункт М. Согласно рис. 11 К = 0,1,2,3, М = 1,2,3,4, причем перевозки возможны лишь в пункт с большим номером. Значит, всего имеется 9 переменных ХKM , а именно, Х01 , Х02 , Х03 , Х12 , Х13 , Х14 , Х23 , Х24 , Х34 . Задача линейного программирования, нацеленная на максимизацию потока, имеет вид:
