Теория управления. Принципы системного анализа

Таким же образом осуществляется оценка предпочтений ЛПР/эксперта относительно остальных критериев путем заполнения еще пяти аналогичных матриц размерностью 3x3. После чего метод парных сравнений распространяется на множество самих критериев относительно Цели - покупки дома. В этом случае ЛПР/эксперту задается следующий вопрос: насколько важнее один критерий (например, размер дома) для Реализации цели по сравнению с другим (например, финансовые условия)? Как следует из иерархии, размерность этой таблицы 6x6.

Принимая во внимание свойство матрицы, т. е.:

и, как следствие, rii=1, количество вопросов равно n*(n-1)/2

Формализацией понятия непротиворечивости для метода парных сравнений является выполнение следующего равенства:

r*ij = r*ik  r*kj i,j,k (1)

где r*ij - это элементы матрицы полученные в результате идеально согласованного эксперимента. Соотношение (1) соответствует правилу логического вывода, которое в этом случае формулируется следующим образом: если i-й объект предпочтительнее k-го объекта на r*ik и k-й объект предпочтительнее j-го объекта на r*kj , то i-й объект предпочтительней j-го объекта на r*ij, причем r*ij = r*ik  r*kj .

Теорема. Если матрица R* обладает свойством (1), то тогда существуют такие числа *i > 0, что имеет место равенство:

(2)

Числа отождествляются с весами дуг (это множество W в графе G) либо с весами объектов первого уровня (это Zi, i  V1).

Матрица R* имеет единичный ранг, , собственный вектор матрицы, где n - соответствующее ей собственное число.

Действительно,

(3)

Практически добиться полной согласованности (т.е. непротиворечивости) суждений ЛПР/эксперта далеко не всегда возможно. Поэтому в общем случае rij будут отклоняться от "идеальных"

вследствие чего соотношения 1, 2, 3 не будут иметь место.

Для дальнейшего анализа полезными являются следующие два факта из теории матриц:

-Во-первых, если 1, ., n , являются собственными числами матрицы R и если

Согласно этому утверждению, если имеет место (3) (т.е. матрица является идеально согласованной), то все собственные числа ее - нули, за исключением одного, равного n.

-Во-вторых, если элемент положительной обратносимметричной матрицы R незначительно изменить, то собственные числа этой матрицы также изменятся незначительно, т.е. они являются непрерывными функциями ее элементов.

Объединяя эти результаты, находим, что при малых изменениях rij от r*ij наибольшее собственное число max (практически получаемой матрицы R при использовании метода парных сравнений) остается близким к n, a остальные собственные значения - близкими к нулю.

Отсюда можно сформулировать следующую задачу: для нахождения весов дуг или объектов первого уровня по полученной в результате метода парных сравнений матрице R необходимо определить собственный вектор , соответствующий максимальному собственному числу, т.е. решить уравнение :

(4)

Так как малые изменения в вызывают малое изменение max, отклонение последнего от n является мерой согласованности. Она может быть выражена с помощью индекса согласованности (ИС):

(5)

Если ИС 0,1, то практически считается, что мера согласованности находится на приемлемом уровне.

Индекс согласованности матрицы парных сравнений, элементы которой сгенерированы случайным образом, называется случайным индексом (СИ). Ниже представлена таблица соответствия порядка и среднего значения СИ, определенная на базе 100 случайных выборок.

Таблица средних значений СИ

Отношение ИС к среднему СИ для матрицы того же порядка называется отношением согласованности (ОС). Значение ОС меньшее или равное 0,10 считается приемлемым. Обычно ИС и ОС указываются в процентах. Согласно определению, ИС можно трактовать как отклонение от идеально проведенного эксперимента (метода парных сравнений), а ОС указывает, на сколько оцениваемая степень согласованности сходится со степенью согласованности самого неидеально проведенного эксперимента.

Таким образом, МАИ допускает несогласованность (как неотъемлемую часть метода), признавая, что человеческие суждения находятся в постоянном процессе изменения и эволюции (поэтому не следует настаивать на 100% согласованности, так как суждения могут измениться после того, как проблема решена). Но надежные решения не могут быть приняты без приемлемого уровня согласованности.

Существуют два метода решения уравнения RV = maxV .Это прямой и итерационный.

Рассмотрим прямой метод. Проверим алгоритм данного метода. R - идеально согласованная матрица, т. е.

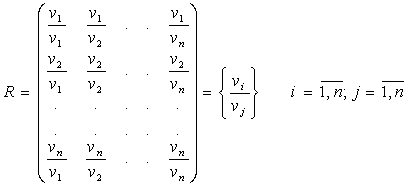
1. Определим среднее геометрическое каждой строки R:

2. Вычислим сумму средних геометрических

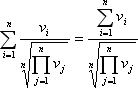
4. Разделим среднее геометрическое каждой строки R на сумму средних геометрических строк:

5.