F → max ,
Х01 + Х02 + Х03 = F (0)
- Х01 + Х12 + Х13 + Х14 = 0 (1)
- Х02 - Х12 + Х23 + Х24 = 0 (2)
- Х03 - Х13 - Х23 + Х34 = 0 (3)
- Х14 - Х24 - Х34 = - F (4)
Х01 ≤ 2
Х02 ≤ 3
Х03 ≤ 1
Х12 ≤ 4
Х13 ≤ 1
Х14 ≤ 3
Х23 ≤ 1
Х24 ≤ 2
Х34 ≤ 2
ХКМ ≥ 0 , К, М = 0, 1, 2, 3, 4
F ≥ 0 .
Здесь F - целевая функция, условие (0) описывает вхождение грузов в транспортную систему. Условия (1) - (3) задают балансовые соотношения для узлов 1- 3 системы. Другими словами, для каждого из внутренних узлов входящий поток грузов равен выходящему потоку, грузы не скапливаются внутри и системы и не "рождаются" в ней. Условие (4) - это условие "выхода" грузов из системы. Вместе с условием (0) оно составляет балансовое соотношение для системы в целом ("вход" равен "выходу"). Следующие девять неравенств задают ограничения на пропускную способность отдельных "веток" транспортной системы. Затем указана неотрицательность объемов перевозок и целевой функции. Ясно, что последнее неравенство вытекает из вида целевой функции (соотношения (0) или (4)) и неотрицательности объемов перевозок. Однако последнее неравенство несет некоторую общую информацию - через систему может быть пропущен либо положительный объем грузов, либо нулевой (например, если внутри системы происходит движение по кругу), но не отрицательный (он не имеет экономического смысла, но формальная математическая модель об этом "не знает").
Лекция 11. Основные положения теории планирования экспериментов
Поверхность отклика
Планирование эксперимента позволяет оптимизировать трудовые, временные и материальные затраты на проведение исследований, обеспечить их наиболее эффективное выполнение, а отсутствие соответствующего плана может существенно повысить трудоемкость исследований или сделать экспериментальную программу полностью безрезультатной.
Исторически теория планирования эксперимента начала развиваться с факторного планирования, основы которого зародились еще в 30-х годах XX столетия. Основы этой теории состоят в построении экономичных планов, по результатам экспериментальных измерений в точках которых можно делать статистические выводы о неизвестных параметрах функций регрессии, причем делать это на основе четко формализованных процедур. Факторное планирование включает построение полных и дробных факторных планов, ортогональных латинских квадратов и сбалансированных блок-схем. В отличие от классического эксперимента, в котором влияние различных значений входных переменных на результаты исследования рассматривается по одному при факторном планировании эти значения одновременно комбинируются в разных вариантах. Это позволяет дать более точные оценки неизвестных параметров регрессии при равном числе измерений.
К настоящему времени сложилась стройная теория планирования эксперимента, оперирующая с достаточно сложным математическим аппаратом, имеющая свою терминологию. Здесь мы рассмотрим лишь основные положения этой теории, позволяющие организовать процесс моделирования не очень сложных систем. При этом мы ограничимся рассмотрением двухуровневых планов, в которых влияние на результат эксперимента каждой из входных переменных изучается на двух уровнях, т.е. при наименьшем и наибольшем значениях этой переменной в пределах исследуемой области. Двухуровневые планы в силу ряда преимуществ получили наибольшее распространение при факторном планировании эксперимента.
Поскольку математические методы планирования эксперимента основаны на кибернетическом подходе, наиболее подходящей моделью эксперимента является «черный ящик», для которого известно лишь то, что подается на его вход, и то, что получается на выходе, а устройство этого ящика значения не имеет. Соответственно мы будем иметь два типа переменных (входных и выходных), которые называют факторами и откликами. Для выяснения различий между ними рассмотрим простой эксперимент, в котором рассматриваются лишь две переменные x и y и целью которого является ответ на вопрос: как при изменении x будет изменяться у В этом случае x – фактор, а у – отклик. В литературе встречаются другие термины: для фактора – режим, независимая переменная, входная переменная, экзогенная переменная; для отклика – реакция, выход, зависимая переменная, переменная состояния, эндогенная переменная. Подобная терминология возникла в связи с тем, что первые исследования с применением статистических экспериментов проводились в сельском хозяйстве, биологии, а затем стремительно вторгались в другие ниши, пополняясь там терминами, наиболее близкими и понятными читателям.
Каждый фактор xi может принимать в эксперименте одно из нескольких значений, называемых уровнями. Каждому уровню соответствует определенная точка в многомерном пространстве, а множество таких точек образует поверхность отклика. На рис. 1 показана поверхность отклика для двухфакторного эксперимента. Факторами являются переменные х1 и х2. В точках 1, 2, 3, 4 эти факторы принимают определенные значения, которым отвечают соответствующие точки на поверхности отклика.
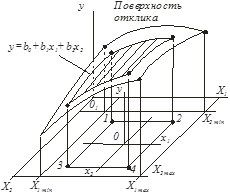
Рис. 1.Поверхность отклика
Конфигурация поверхности отклика, следовательно, функция не известна. Целью
![]() (1)
(1)
эксперимента является либо описание этой поверхности (хотя бы приближенное) в интересной для исследователя области варьирования факторов, либо определение экстремального значения отклика. Вторая задача может быть сведена к пошаговому выполнению первой, поэтому на начальном этапе нас будет интересовать только поиск аналитического выражения, близкого к искомой функции (1) в заданной области. Этот поиск осуществляют на основе обработки экспериментальных данных в точках 1, 2, 3, 4 (рис. 3.3) факторного пространства.
Этапы планирования эксперимента
Общая схема планирования экспериментов для решения экстремальных задач состоит из следующих этапов:
1) постановка задачи;
2) выбор параметра оптимизации;
3) выбор факторов;
4) составление линейного плана;
5) реализация линейного плана и построение линейной модели;
6) поиск области экстремума;
7) описание области экстремума;
8) интерпретация результатов.
Постановка задачи. Решение любой задачи начинается с ее формулировки. При этом необходимо иметь ясное, четкое и вполне однозначное представление о цели работы. Желательно, чтобы эта цель была сформулирована количественно, так как планирование экспериментов связано прежде всего с установлением количественных связей между входными и выходными параметрами изучаемой системы. Разумеется, объект обследования должен быть управляемым.
Выбор параметра оптимизации. Одним из наиболее ответственных этапов является выбор параметра оптимизации. Он должен быть однозначным, характеризоваться числами, действительно определять оптимум. Надо стремиться к тому, чтобы параметр был только один, имел ясный физический смысл и оценивался с максимальной статистической эффективностью (последнее позволяет сократить до минимума число параллельных опытов).
