Теория управления. Принципы системного анализа

Таблица 10.3

Рассмотрим второе уравнение системы (13), которое будет справедливо для М-матрицы (14), но с некоторым отличием. Это отличие связано с тем, что было построено фиктивное дерево, поэтому в ветвях его не будет токов и, следовательно, исходное уравнение примет вид . Индекс «х» у вектора J мы опустили, поскольку хордами являются все ребра исходного графа. Обратите внимание, что транспонированная М-матрица представляет собой не что иное, как матрицу инциденций исходного графа (см. рис.), записанную с обратными знаками:

(15)

Все это позволяет записать второе уравнение системы (13) в ином виде: .

Первое уравнение системы (13) изменится следующим образом. Разность потенциалов ветвей дерева Uvd есть разность потенциалов i-й и базовой точек, т. е. потенциал i-й точки . М-матрица будет равна , поэтому первое уравнение системы (13) примет вид .

Все сказанное дает возможность записать систему уравнений (13) в следующей форме:

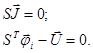(16)

Таким образом, возможны два способа формализации процедур построения математической модели для описания эквивалентной схемы технического объекта, в одном из которых используют систему уравнений (13) и М-матрицу, в другом – систему уравнений (16) и матрицу инциденций ориентированного графа.

В качестве примера рассмотрим механическую систему (рис. 14, а), эквивалентная схема (б) и граф (в) которой изображены на рисунке. Матрица инциденций приведена в табл. 3.

Таблица 3

Рис. 14.К примеру механической системы

Первое уравнение (16) в развернутой форме имеет вид:

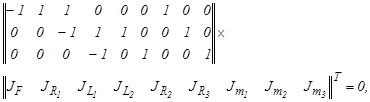
где потоковые переменные JR, JL, Jm=Jc типов R, L, С можно записать в форме приведенных выше зависимостей между фазовыми переменными. В результате будет получена система дифференциальных уравнений. Транспонируя матрицу инциденций и используя второе уравнение системы (16), аналогично можно получить систему дифференциальных уравнений для переменных типа потенциала.

Лекция 18. Многокритериальная оптимизация

Свойства задач принятия решения со многими критериями

В технической практике задачи ПР с учетом нескольких критериев возникают достаточно часто. Сложность подобных задач существенно выше, чем при наличии одного критерия. Если при этом еще учитывать и неоднозначность внешних воздействий, то для получения корректного результата кроме математических знаний необходим также и опыт в соответствующей предметной области.

Теоретически можно представить случай, когда во множестве окажется одна альтернатива, для которой все r критериев (целевых функций) принимают наибольшие значения (в предположении, что все критерии максимизируются). Естественно, что данная альтернатива и будет наилучшей. К сожалению, на практике такие ситуации практически не встречаются, а типичным является случай, представленный на рис. 1, для двух целевых функций.

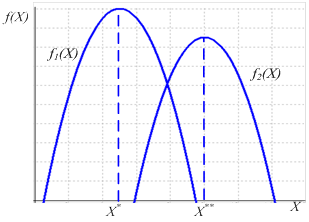
Рис. 1. Ситуация ПР для двух критериев

При Х* максимума достигает одна целевая функция, а при Х** – другая; нам же предстоит сделать только один выбор. Очевидно, что ППР здесь становится менее прозрачным.

Сформулируем некоторые очевидные положения для подобных ситуаций:

1. Не существует результата наилучшего в абсолютном смысле.

2. Решение может считаться лучшим лишь для конкретного ЛПР, с учетом его предпочтений.

3. Для нахождения приемлемого результата должна строиться многокритериальная модель, которая создается для уточнения предпочтений ЛПР. Она должна быть логически непротиворечивой и должна включать в себя основные свойства решаемой задачи.

Прежде чем переходить к рассмотрению многокритериальных задач, остановимся на предпосылкахих постановки, т.е. укажем причины, порождающие проблему многокритериальности. Для этого обратимся к блок-схеме, приведенной на рис. 2 в лекции 2 (рис. 2). Данная схема отражает рациональную логическую последовательность этапов при подготовке и принятии решений.

С проблемой многокритериальности лицо, принимающее решение, сталкивается на этапе 7 (Выбор наиболее предпочтительного вариата решения). Вместе с тем, ЛПР на более ранних этапах (2 и 3 при формулировании цели и критериев оценки) сам предопределяет постановку многокритериальной задачи. Следовательно, предпосылкой постановки многокритериальной задачи является необходимость проведения этапа 3 (формирования системы критериев). Этот этап может и отсутствовать, если цель принятия решения четко определяется одним критерием.