Решение. Запишем уравнение регрессии для линейной поверхности отклика
(13)
Коэффициенты bi будем определять по формуле (3.4) в соответствии с приемами, указанными в пояснениях к этой формуле.
Вначале определим коэффициенты регрессии, используя данные полного факторного эксперимента (левую часть табл. 5). Будем иметь:
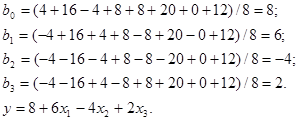(14)
Построим дробные реплики, для чего заполним правую часть табл. 5 (столбцы 7 .10) и выберем строки, у которых 10-й столбец имеет одинаковые знаки. В результате получим две полуреплики (таблица 6):
Таблица 6
|
№ опыта |
x0 |
x1 |
x2 |
x3 |
y |
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Первая полуреплика | |||||
|
2 |
+1 |
+1 |
-1 |
-1 |
16 |
|
3 |
+1 |
-1 |
+1 |
-1 |
-4 |
|
5 |
+1 |
-1 |
-1 |
+1 |
8 |
|
8 |
+1 |
+1 |
+1 |
+1 |
12 |
|
Вторая полуреплика | |||||
|
1 |
+1 |
-1 |
-1 |
-1 |
4 |
|
4 |
+1 |
+1 |
+1 |
-1 |
8 |
|
6 |
+1 |
+1 |
-1 |
+1 |
20 |
|
7 |
+1 |
-1 |
+1 |
+1 |
0 |
Определим коэффициенты регрессии по дробным репликам.
Для первой полуреплики будем иметь:
b0 = (16 - 4 + 8 + 12) / 4 = 8;
b1 = (16 + 4 - 8 - 12) / 4 = 6;
b2 = (-1б - 4 - 8 + 12) / 4=-4;
b3 = (-16 + 4 + 8 + 12) / 4 = 2.
Для второй полуреплики будем иметь
b0=(4 + 8 + 20 + 0) / 4=8;
bl=(-4+8+20-0)/4=6;
b2 =(-4+8-20+0)/4=-4;
b3 = (-4-8 + 20)/4=2.
Как и следовало ожидать, во всех трех случаях для линейной поверхности отклика получены одинаковые результаты.
На рис. 2 приведена схема полного трехфакторного эксперимента и его полуреплик. Цифрами отмечены номера опытов с указанием в скобках координат факторов x1, x2,x3. Точки 2, 3, 5, 8 соответствуют первой полуреплике, а цифры I, 4, 6, 7 – второй. Обратите внимание, что каждая из полуреплик наиболее полно охватывает опытные точки факторного пространства.
Рис. 2.Схема трехфакторного эксперимента
При большом числе факторов т для оценивания параметров линейной функции регрессии (1) можно строить дробные реплики высокой степени дробности. Так, при т=7 можно построить дробную реплику из полного факторного плана 23 для первых трех факторов, приравняв четыре остававшихся фактора к двухфакторным и трехфакторному взаимодействиям трех других факторов, положив, например
(15)
Такую реплику записывают как 27-4.
В общем случае дробную реплику обозначают через 2т-p, если р факторов приравнены к произведениям остальных т—p факторов, уровни которых выбраны согласно полному факторному плану. Дробную реплику 2т-p можно строить различными способами. Для анализа системы смешивания коэффициентов пользуются понятиями генерирующих и определяющих соотношений.
Генерирующими называют соотношения, с помощью которых построена дробная реплика. Так, для реплики, представленной в табл. 5, генерирующим является соотношение х3=x1х2, а это указывает, что фактор х3 занимает в матрице столбец, соответствующий взаимодействию x1x2. Для указанной выше реплики 27-4 генерирующим является соотношение (15).
Определяющим соотношением (определяющим контрастом) называют равенство, в левой части которого стоит единица, а в правой — какое-либо произведение факторов. Для дробной реплики 2т-p можно получить p различных определяющих соотношений из генерирующих путем умножения обеих частей последних на их левые части с последующей заменой (хi)2 на 1 (i=1, , т). Другие определяющие соотношения получаются путем перемножения ранее полученных и выделения среди них новых. Например, для реплики (табл. 5) определяющим является соотношение (12).
Построим определяющие соотношения для реплики 27-4, задаваемой генерирующими соотношениями (15). Умножая обе части равенств (15) на их левые части, получаем четыре определяющих соотношения:
(16)
Попарное перемножение этих четырех соотношений дает шесть новых:
(17)
Перемножение каждой тройки из четырех соотношений (16) Дает еще три определяющих соотношения:
(18)
Наконец, перемножая все четыре соотношения (16), получаем
(19)
Легко понять, что кроме (16) – (19), других определяющих соотношений для рассмотренной реплики 2+7-4 нет.
Знание определяющих соотношений позволяет найти всю систему совместных оценок без изучения матрицы планирования дробной реплики. Для того чтобы определить, с какими взаимодействиями смешано данное, нужно на него умножить обе части всех определяющих соотношений.
Определим, например, с какими взаимодействиями смешан главный эффект b3 в дробной реплике 27-4, определяемой генерирующими соотношениями (15). Для этого умножим все определяющие соотношения (16) – (19) на х3. Получим
Следовательно, главный эффект b3 смешан с эффектами взаимодействий первого порядка 
с эффектами взаимодействий второго порядка 
третьего порядка 
четвертого порядка 
и пятого порядка 
Скачать реферат