Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда динамики выражаются в виде функции времени 
. Выбор функции производиться на основе анализа характера закономерностей динамики числа вызовов.
Если характер динамики подтверждает предложение о том, что уровень явления падает с более или менее постоянной абсолютной скоростью, т.е. с относительно стабильными ценами абсолютного прироста, то математическим выражением такой тенденции будет являться прямая линия.
Аналитическое уравнение прямой применительно к выравниванию.
(6)
где
- выровненные уровни;
t - время, т.е. порядковый номер интервала или момента времени; 
- параметры прямой.
Параметры и искомой прямой, удовлетворяющие принципу наименьших квадратов, находят путем решения следующей системы нормальных уравнений:
(7)
(8)
где y - фактические (эмпирические) уровни ряда динамики;
n -число уровней;
t -время (порядковый номер интервала или момента времени).
Для выравнивания ряда динамики по прямой за начало отсчета времени примем центральный интервал рассматриваемого этапа. При нечетном числе уровней получим следующие значения t:
|
годы |
2003 |
2004 |
2005 |
2006 |
2007 |
|
t |
-2 |
-1 |
0 |
1 |
2 |
Таким образом
(9)
в результате этого система уравнений примет вид:
(10)
(11)
Откуда
(12)
(13)
Для подсчета необходимых сумм (
,
,
,
) составим расчетную таблицу:
Таблица 3 - Расчет выровненных уровней 
|
Годы |
Число вызовов (у) |
Обозначение времени |
у∙t |
t2 |
у2 |
Выровненные уровни
|
|
1 |
3108 |
-2 |
-6216 |
4 |
9659664 |
2669,6 |
|
2 |
2946 |
-1 |
-2946 |
1 |
8678916 |
2562,7 |
|
3 |
2019 |
0 |
2019 |
0 |
4076361 |
2455,8 |
|
4 |
2338 |
1 |
2338 |
1 |
5466244 |
2348,9 |
|
5 |
1868 |
2 |
3736 |
4 |
3489424 |
2242 |
|
Σ |
12279 |
0 |
-1069 |
10 |
31370609 |
12279 |
Подставляя в формулы (12, 13) итоговые суммы из табл. 3, получим:
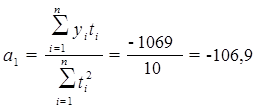
Отсюда уравнение искомой прямой будет:
Путем подстановки в это уравнение соответствующих значений найдем выровненные уровни
Так, для 3 ( t = 0) получим:
= 894,125 + 38,10119 = 2455,8
Рассчитаем выровненные уровни для остальных годов. Результаты расчета занесем в таблицу (3).
Найдем сумму выровненных уровней:
= 2669,6 + 2562,7 + 2455,8 + 2348,9 + 2242 =12279
Как видно из сравнения итогов граф 2 и 7 табл. 3, значения сумм 
и 
равны, что свидетельствует о правильности расчетов для определения параметров 
и 
уравнения.
О качестве построенной математической модели можно судить по так называемому коэффициенту корреляции R, вычисляемому по следующей формуле
Скачать реферат