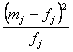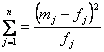Применение математических методов в государственной противопожарной службе

Pj {tj _ t обсл _ tj+1} = (35)

Данные вычислений сводятся в таблицу

Эмпирическое распределение времени занятости пожарных подразделений обслуживанием вызовов

На основании вычислений определяется критерий Романовского

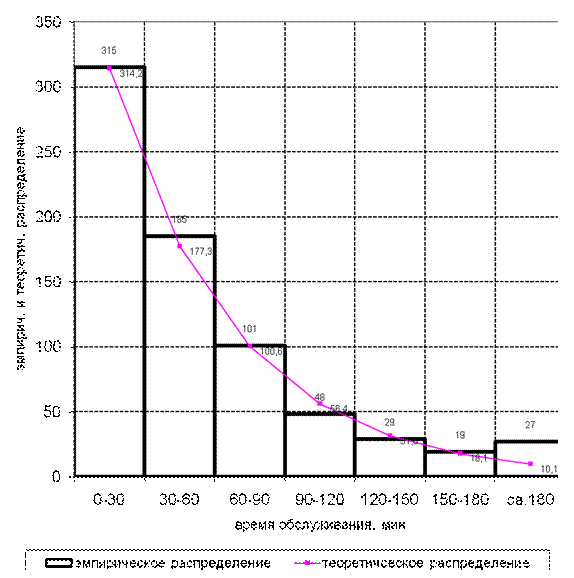
Графики эмпирического и теоретического распределений длительности времени обслуживания вызова.

Моделирование одновременного возникновения пожаров

Вызовы, обслуживание которых происходит в один и тот же промежуток времени, называются одновременными.

Для рациональной организации оперативной деятельности подразделений ГПС в городе необходима правильная оценка возможностей пожарных подразделений обслуживать вызовы.

В процессе функционирования подразделений ГПС в городе особо важно предвидеть ситуации, требующие одновременного обслуживания нескольких вызовов. Такие критические ситуации характеризуются повышенной, а иногда предельной напряженностью функционирования пожарных подразделений.

Рассмотрим множество возможных состояний подразделений ГПС в городе, обозначаемых Ео, Е1, Е2, Е3,…, и пронумерованных по числу вызовов, обслуживанием которых заняты подразделения ГПС. В произвольный момент времени подразделений ГПС в городе могут находится в одном из этих состояний Еm (m=0,1,2,3,…). В дальнейшем возможны переходы из состояний Еm в состояние Еm-1 (в случае «освобождения» ПП от обслуживания одного из m вызовов) или в состояние Еm+1 (в случае возникновения еще одного вызова). Так как моменты возникновения вызовов и «освобождения» ПП от обслуживания их являются случайными, то и процесс возникновения одновременных вызовов имеет случайный характер и ему свойственны вероятностные закономерности.

Вероятность Рm того, что в произвольный момент времени подразделения ГПС в городе находятся в состоянии Еm одновременного обслуживания m вызовов, вычисляется по формуле:

(37)

где: a - параметр, называемый приведенной плотностью потока вызовов.

Расчет параметра a осуществляется по формуле:

(38)

При использовании формулы (37) размерность единиц измерения времени в величинах l и tобсл. должно быть согласована.

Для последовательных вычислений вероятностей Р0, Р1, Р2, Р3, … удобно использовать рекуррентные формулы, получаемые из формулы (38)

Ожидаемое на протяжение единичного промежутка времени число fm случаев, когда при возникновении очередного вызова возникает потребность в одновременном обслуживании того или иного числа m вызовов (т.е. число переходов из состояния Еm-1 в состояние Еm), вычисляется по формуле:

(m = 1, 2, 3, …) (39)

Между значениями Рm и fm имеют место следующие соотношения, которые могут быть использованы для проверки правильности вычислений:

(40)

Время, в течении которого в городе одновременно обслуживается «m» вызовов определяется по формуле:

Тm=Т'Рm , (41)

где: Т - время наблюдения за процессом функционирования подразделений ГПС.

Для наглядности теоретическое и эмпирическое число переходов системы состояния Еm в состояние Еm+1 сводятся в таблицу.

Теоретическое и эмпирическое число переходов системы состояния Еm в состояние Еm+1