Применение математических методов в государственной противопожарной службе

Страница
2

Рефераты / Применение математических методов в государственной противопожарной службе

В процессе анализа динамических рядов трудно обойтись без обобщающих показателей, в качестве которых выступают различного рода средние, рассчитываемые как по уровням, так и по производственным показателям ряда. Подобного рода средние, подсчитанные по смежным уровням динамического ряда, называются динамическими или хронологическими.

Динамические средние должны подсчитываться в пределах качественно однородных периодов и на основе исчерпывающих данных за весь однородный период от начала до конца. Иначе говоря, здесь мы наблюдаем известное методологическое требование об однородности и полноте данных при исчислении средних величин.

Рассмотрим особенности исчисления динамических средних для уровней и производственных показателей по формуле средней арифметической простой:

(6)

- средний уровень ряда;

Yi – уровень ряда;

ti – длительность отдельных интервалов времени ( если они различны);

- общая численность совокупности.

Если интервалы времени равны то формула (6) примет вид:

(7)

где n – число равных промежутков или интервалов времени.

Средний абсолютный прирост подсчитывается по формуле:

(8)

где: Yn – конечный уровень динамического ряда;

Yб – базисный уровень.

В случае равенства интервалов формула (8) принимает вид:

(9)

Средний темп прироста подсчитывается по формуле средней геометрической, что объясняется особенностью получения показателя общего темпа роста за весь период времени (он равен произведению отдельных темпов).

В случае равных интервалов времени средний темп прироста определяется по формуле средней геометрической простой, которая имеет вид:

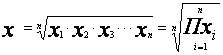(10)

где: xi – коэффициент роста за определенный интервал времени ti;

n – число равных интервалов времени;

ti – интервал времени;

П – знак произведения.

Выявим тенденцию ряда динамики, которая позволяет представить ее изменение за анализируемый период времени в виде некоторой модели.

Наиболее эффективным способом выявления тенденции ряда динамики является аналитическое выравнивание. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:

, (11)

где - уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени t.

Определение теоретических (расчетных) уровней производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики. Для выбора вида функциональной зависимости используется прием, основанный на том, что определенные соотношения между изменениями входной и выходной величины предполагают ту или иную функциональную зависимость.

Если выполняется условие:

то принимается линейная модель ,

где - коэффициенты, определяемые по МНК (метод наименьших квадрантов);

- приращения зависимой и независимой переменной, то есть .

· , то принимается модель ,

· , то ,

· , то

· , то .

Следующим этапом является расчет параметров выбранной экстраполяционной функции.

В качестве метода оценки параметров применяется метод наименьших квадратов, сущность которого состоит в отыскании параметров модели тренда, минимизирующих ее отклонение от точек исходного ряда, то есть

, (12)

где - расчетные значения исходного числового ряда;

- фактические значения исходного ряда;

n – число наблюдений.

Если модель тренда представить в виде:

, (13)

где - параметры модели; t – время; - независимые переменные, то для того, чтобы найти параметры модели, удовлетворяющие условию (7), необходимо приравнять нулю первые производные величины S по каждому из коэффициентов . Решая полученную систему уравнений с неизвестными, находим значения коэффициентов .

Рассмотрим технику выравнивания ряда динамики:

· по прямой:

Параметры a и b согласно МНК, находятся решением следующей системы нормальных уравнений, полученного путем алгебраического преобразования условия (12).

(14)